211pg. 앙상블
여러개의 Classifier를 생성하고 그 예측을 결합하여 정확한 최종 예측을 도출하는 기법. 정형데이터 분류에 성능이 좋다.
- 앙상블 유형: Voting(하드보팅, 소프트보팅), Bagging(랜덤포레스트 알고리즘), Boosting(그래디언트 부스트, EGBoost, LightGBM 모듈), Stagging(메타모델 재학습)
- Voting방식: Data Set를 각각의 분류기가 학습을 한다. 서로 다른 Estimator를 사용하는 경우가 많음. 하드보팅은 다수결 원칙으로, 소프트보팅은 평균적인 확률값이 높은 것을 원칙으로 예측값을 도출한다.
- Bagging방식: Data Set를 샘플링해서 각각의 분류기가 학습을 한다. 서로 동일한 Estimator를 사용하는 경우가 많음.
참고) 이항분포 확률질량함수를 이용해 분류기의 개수 차이에 따른 퍼포먼스 Voting방식 차이점을 알아보자.
동전던지기에서 앞면이 나올 확률 0.5, 뒷면이 나올 확률 0.5이라고 할 때 동전을 던지는 회수를 증가시킬수록 앞면이 나올 확률은 0.5에 수렴한다. 이와 같은 맥락에서 Hardvoting의 경우 분류기의 개수가 많아지면 정답값을 예측하는 확률에 가까워진다(정답의 비율이 절반 이상이 될 확률이 높음). 즉 분류기의 개수가 많을수록 본연의 estimator확률에 수렴하게 된다.
이항분포 확률질량함수: n번 시행 중 k번 성공할 확률

누적이항분포 확률질량함수: x번을 시행했을 때 j번 이상 성공할 확률 ( j~x번까지 실행 했을 때 성공할 확률을 다 더한 값

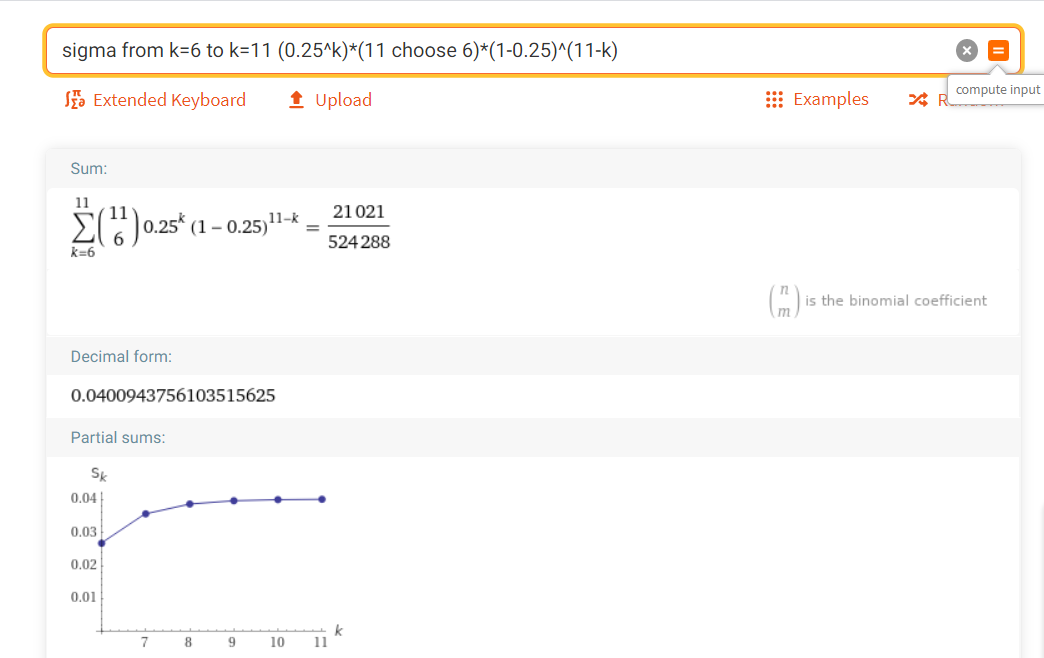
Wolframalpha 접속 후 다음과 같이 계산한다.
Wolfram|Alpha: Making the world’s knowledge computable
Wolfram|Alpha brings expert-level knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels.
www.wolframalpha.com
sigma from k=6 to k=11 (0.25^k)*(11 choose 6)*(1-0.25)^(11-k)
(설명: 0.25은 11번 중 6번 이상 성공할 확률/에러가 발생할 확률 (관점에 따라 다름))
앙상블 실습 (책에 없는 내용)
- n_classfier를 2로 나눈 값을 math.ceil (올림함수)한 것을 int값으로 받는다.
- comb(x, y)는 x번 중 y실행하는 경우의 수를 말한다.
- range는 6부터 11까지의 값을 가지고 있다. probs는 for문의 output값을 말한다. (이항분포 확률질량함수)
- error**k는 error의 k승을 말한다. (=error^k)
- sum(probs)는 각각의 probs (확률값)을 더한 누적이항분포 확률질량함수를 말한다.

누적이항분포 확률질량함수 ensemble_error(n_classifier=11, error=error) 은 11번 시도 중 절반이상(6번 이상) 에러가 발생할 확률인데, error_range (0부터 1까지 0.01스텝으로)의 값에 따라 for문을 돌린 output값이다.
다음을 plt.plot으로 그리면 다음과 같다. 그래프가 의미하는 바는 error 확률이 0.5보다 작으면 누적이항분포질량함수가 낮고, 0.5보다 높으면 누적이항분포질량함수가 높다는 것이다. (참고로 error가 0.5보다 클 확률은 실질적으로 많이 존재하지 않아서 0.5이상 값을 볼 필요는 없다.) error확률이 20%인 (성공확률이 80%) estimator 11개를 가지고 (즉, 앙상블로) voting방식을 사용하면 error확률이 단일 estimator 사용보다 낮아진다는 것을 의미한다.

scipy 실습 (책에없음)
(scipy=mathworks의 저렴이버전)
- 59줄: binom.pmf(이항분포 확률질량함수)는 성공확률이 0.5일 때 2번의 시행 중 1번 성공할 확률을 return한다.
- 62줄: binom.rvs(랜덤표본생성)는 성공확률이 0.2일 때 10번의 시행을 하는 것을 5번 수행(size=5)한 것을 random하게 return한다. (seed: 랜덤값을 만드는 규칙1을 말한다.) 62줄만 단독 시행하면 [ 2 3 0 1 1]이라고 나오는데, 이는 10번 시행했을 때 성공이 2번, 3번, 0번, 1번, 1번임을 의미한다.

- 73줄: binomial.pmf와 같은데, k=m으로 설정하면 성공확률이 0.2를 10번 실행했을 때, 0-9번 성공할 확률을 적용해서 이항분포 확률질량함수를 각각 계산한다.
- 76줄: distplot(히스토그램 함수)에서 bins의 m은 0-9까지 성공하는 횟수를(x축), norm_hist는 정규화 유무, kde는 추세곡선을 의미한다.

20% 성공할 확률이 10번 시행했을 때 0-2번 성공할 확률이 가장 높고 점점 작아진다.

참고) 67줄: binomial.rvs(size=x) 시행횟수 사이즈를 증가시키면 그래프는 점점 pmf값에 수렴하게 된다. (pmf 확률적 이론값/예측값과 실제 값이 수렴하게 됨)
binomial.rvs(size=10)

binomial.rvs(size=100)

binomial.rvs(size=10000)

- 80줄: cdf(누적이항분포 확률질량함수)에서 성공확률이 0.51인 것을 10000번 시행했을 때 4999(0~4999까지의 이항확률질량함수를 다 더한 값)이하의 누적확률값을 의미한다. 그런데, 여기서 1-sp.stats.binom.cdf이므로 결국 5000번 이상 성공할 확률의 누적이항분포 확률질량함수를 의미한다.
좀 더 자세히 말하면, 분류기 10000개가 각각 시행되었을 때 4999번 성공했음( sp.stats.binom.cdf)은 과반수를 넘지 않아서 실패할 확률, 즉 에러율이라고 볼 수 있다.(10000번 중 1번 올바르게 예측할 확률, 2번 올바르게 예측할 확률 ......4999번 올바르게 예측할 확률이므로)
즉 1-sp.stats.binom.cdf는 10000번 시행했을 때 5000번-10000번 이상 올바르게 예측할 확률의 누적확률값을 말한다. 즉 50%이상이므로 올바르게 예측할 확률을 말한다. 이는 다수결원리로 예측값을 도출하는 hardvotting과 연결해서 생각할 수 있다.
(성공확률 p값과는 관련없이 k값에 의해 분류기의 성공확률이 결정된다. 즉, k값이 n의 과반수 이상이 되어야 분류기가 성공적으로 예측했다고 말한다)

10000개의 분류기가 과반수 이상이 올바르게 예측할 확률(분류기의 성공확률)은 97.8% 라는 결과가 나온다.
- Hardvotting/Softvotting 방식 비교

- classifiers의 데이터 타입은 estimator이다. (element 3개가 다 estimator, pipe1, clf2, pipe2)
- 다음과 같은 에러는 105줄을 import six로 코드를 바꾸면 된다.

- 90줄: bincount는 각각의 인덱스 포시션의 개수를 나타낸다. weights는 각각의 포지션의 가중치 값을 말한다.
print(np.bincount([0, 0, 1]))는 0 index포지션의 값이 2개임을 1 index포지션의 값이 1개임을 나타낸다. [2,1]이라고 출력됨. print(np.bincount([0, 0, 1, 3, 3, 3]))는 [2, 1, 0, 3]이라고 출력됨. (0인덱스 포지션 2개, 1인덱스 포지션 1개, 2인덱스 포지션 0개, 3인덱스 포지션 3개이므로)
print(np.bincount([0, 0, 1], weights=[0.2, 0.2, 0.6]))는 각각의 포지션 개수에 가중치를 부여하여 [0.4 0.6] 가 출력된다.
마찬가지로 print(np.bincount([0, 0, 1, 3, 3, 3], weights=[0.2, 0.3, 0.6, 0.1, 0.1))은 [0.5, 0.6, 0, 0.2]가 출력된다.
- argmax: 가장 큰 값이 있는 포지션의 인덱스를return 하므로 0.6 값의 포지션을 가진 인덱스 1을 return한다.
- np.average(ex, aixs=0): row방향으로 ex행렬의 평균한다. (ex행렬은 가중치가 0.2, 0.2, 0.6이 각각 붙는다.)
- 112줄: Classiclass MajorityVoteClassifier(BaseEstimator, ClassifierMixin) 라는 클래스는 BaseEstimator, ClassifierMixin이라는 클래스를 상속받는다. 이 클래스는 __init__, fit, predict, predict_proba, get_params의 매서드를 포함한다. (__init__는 생성자 constructor로 클래스가 객체를 만들 때 자동으로 만들어진다)
- 137줄: labelencoding된 값들의 유니크한 값 (_.classes_)
- 144줄: fitted_clf는 학습된 estimator가 들어가있음. clones는 원본estimator를 손상시키지 않고 그대로 복사하는 기능
- 150줄: predict은 0, 1값만 (확률값) 가진 predict_proba랑 다르다. predictions에는 3x5 2차원 데이터가 리턴간다. 교차검증에서 50개의 데이터를 10개씩 나눠서 테스하면 각각 5개가 되고 estimator가 3개이기 때문이다. (참고로 검증데이터 중 45개는 fit시키고 5개는 검증을 시키게 된다.)
아래 cross_val_score의 파라미터 scoring=accuracy로 바꿔준 뒤 데이터 구조를 볼 수 있다. classifiers_.T는 전치행렬을 말하며, 이를 적용하면 5x3의 행렬로 변환된다. (각각의 estimator에 대한 예측값을 보기 위해)


-154줄: np.apply_along axis: 주어진 함수를 주어진 축에 적용해서 그 값을 리턴하는 것. lambda x는 arr=predictions 데이터를 기준으로 aixs=1(column방향, 즉 1개의 row씩)으로 적용된다. bincount 각각의 인덱스의 빈도수를 카운트한 뒤 argmax 최대값을 가진 포지션의 인덱스를 반환 >> predict는 Hardvotting방식과 연관 (LabelEncoder를 미리 했어야 argmax를 사용할 수 있음)
- inverse_transform 을 통해 Label Encoder 하기 전 기존 인덱스 값을 다시 반환시킨다.
- 162줄: predict_proba의 X에는 5x2짜리 test데이터가 들어간다. (왜냐하면 50개의 데이터를 cv값 10개로 나누어 테스트 하기 때문이다) classfiers_에는 estimator 3개가 들어가므로 for문이 3번 돌게 된다.
- 163줄: probas에는 3x5x2의 3차원 데이터가 들어간다. (estimator인 pipe1, clf2, pipe3에 의한 확률값) 이를 avg_proba=np.average([robas, axis=0...)한다면 5x2의 2차원의 데이터로 압축이 된다. (0축으로 평균을 내기 때문이다) >> Softvotting방식과 연관 (각 estimator의 확률값의 평균을 냄)

아래 DecisionTree에서 train_test_split을 하고 clf1-3까지 3개의 estimator를 만든 뒤 test_size, random_state, stratify=y, creterion 등의 파라미터 설정값을 정한다. (stratify=y 훈련 세트와 테스트 세트에 있는 클래스 비율이 원본 데이터셋과 동일하게 유지됩니다.)
- 186줄: LabelEncoder( )을 하면 다시 0부터 int값이 들어간다. (데이터 전처리기법으로 iris.data의 값이 1, 2로 되어 있는데 이를 0, 1로 encoder한다)
트레이닝데이터 X값은 (100x2) 행렬이다. 테스트데이터는 (50, ) 행렬이다. test_size가 0.5이며, stratify=y이므로 25개씩 들어간다. (test데이터의 0과 1의 비율이 반반씩 들어가므로, 200x0.5에서 0과 1도 반반씩 들어간다)
- 187줄: fit_transform은 fit(학습)할 때 만들어져서 인코딩된 lable을 바탕으로 기존 데이터를 transform(변환)한다.

pipe는 estimator처럼 사용된다. StandardScaler라는 estimator를 사용하고 RogesticRegression으로 학습한다.
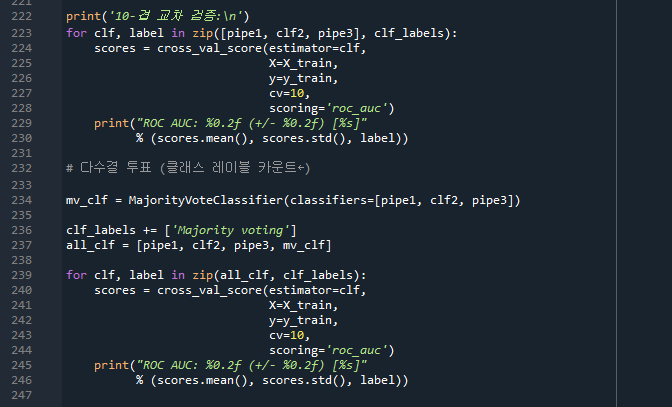
- 240줄: cross_val_score은 자동적으로 교차검증을 수행해준다. (정확도, 정밀도, 재현율 등)
for문에서 pipe1, clf2, pipe3의 값은 for문의 clf값에 들어가고, Logistic regression, Decision tree, KMN은 label값에 들어가 각각 교차검증한다. 즉, voting방식(mv_clf)을 사용하는 estimator 3개(pipe1, clf2, pipe3)를 가지고 교차검증을 한다. (엄밀히 말하면 voting은 아님)

(위의 코드는 난이도가 높아서 대충 어떤 흐름으로 구성되어있는지만 알면 된다)
'살콤아내 자기계발 > 파이썬' 카테고리의 다른 글
| 파이썬 머신러닝 완벽가이드 5주차 정리 (244pg. LightGBM) (0) | 2021.05.18 |
|---|---|
| 파이썬 머신러닝 완벽가이드 5주차 정리 (분류 214pg~, 보팅분류기, 랜덤포레스트, XGBoost) (0) | 2021.05.17 |
| 파이썬 머신러닝 완벽가이드 4주차 정리 (분류 202pg~) (0) | 2021.05.11 |
| 파이썬 머신러닝 완벽가이드 4주차 정리 (분류 183pg~) (0) | 2021.05.07 |
| 파이썬 머신러닝 완벽가이드 3주차 정리 (평가 175pg, Diabetes 실습) (0) | 2021.05.04 |